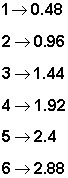
INTRODUCCIÓN A LAS FUNCIONES

La palabra “función”, en un sentido próximo al actual, aparece escrita por primera vez por Leibnitz en 1673 y podríamos decir que un concepto moderno de función no aparece hasta el siglo XIV. Nuestra forma de escribir las funciones como f(x) se debe a Euler,  ya en el siglo XVIII. Sin embargo, el trabajo con dos conjuntos de números, de alguna forma relacionados, es muy antiguo: si bien los babilonios non definieron ni manejaron el concepto de función de una forma moderna, trabajaron con tablas, entre otras, donde aparecían los cuadrados, cubos y recíprocos de los números naturales.

En definitiva,  manejar una función en casos sencillos no es más que disponer de una regla que permita relacionar unos números con otros: calcular el valor del triple de un número, el cuadrado o el seno no son más que ejemplos simples de funciones.

Por ejemplo: una compañía telefónica española de móviles cobra 0.48€ por cada minuto en una llamada. Si hacemos una tabla con el costo de una llamada, algunos de sus valores serían:

Estamos vinculando a cada número de la columna izquierda un número de la columna derecha. Así, a 1 le corresponde 0.6, a 2 le corresponde 1.08, a 3 1.56, etc. Eso mismo lo podríamos escribir de la forma siguiente:

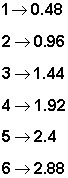
Pero podría continuar escribiendo minutos de llamada y su correspondiente precio. El uso de funciones es útil, por ejemplo, para saber el coste de una llamada de 30 minutos. Lo único que necesitamos saber es la forma de, sabiendo los minutos de la llamada, calcular su coste. Si el número de minutos fuese 20, el coste sería 20×0.48=9.6. Si queremos hacer el cálculo con otra cantidad de minutos, pongamos x, el coste sería x×0.48. Tenemos una función. En concreto:
 

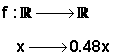
representa los numeros reales, es decir, que los minutos de llamada son un número real y el coste también.

El número de minutos de la llamada varía de una llamada a otra y podemos escoger cuántos minutos llamar. El coste también varía pero dependerá del número de minutos que hablemos. A los minutos que hablamos le llamamos x y le llamaremos variable independiente. Al coste se le llama f(x) (o y) y la llamaremos variable dependiente. Así, si x=3, f(3)=y=1.44, es decir, si el número de minutos ha sido 3, el coste (f(x)) de la llamada es 1.44. Dicho de otro modo, a un x=3 le corresponde un y=1.44.

Pero en realidad, las compañías telefónicas cobran una cantidad fija en cada llamada. El coste de establecimiento de llamada de nuestra compañía es de 0.12€.  La tabla de costes de llamada quedaría por tanto así:
 

Nuestra función sería ahora parecida a la anterior:

f(x)=0.12+0.48x
 

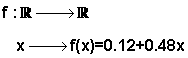
Diagrama cartesiano. Gráfica de una función

Los ejes cartesianos es un sistema que sirve, entre otras cosas, para representar puntos en el plano:

para representar un punto en el plano se necesitan dos números, que se representan sobre dos líneas perpendiculares llamados ejes. El primero se sitúa sobre la línea o eje x (eje de abcisas) y el segundo sobre la línea o eje y (eje de ordenadas). A estos números se le llaman coordenadas del punto y se escriben por orden, separados por una coma y entre paréntesis, (x,y). Primero se escribe la coordenada x, después la coordenada y.  Normalmente se le da por nombre una letra mayúscula del abecedario.  Así, el punto P(2,3) tiene por coordenada x el número 2 y por coordenada y el número 3. Hay, por lo tanto que medir 2 sobre el eje de abcisas y 3 sobre el eje de ordenadas. Después, trazar paralelas a los ejes hasta que éstas se crucen, determinando el punto P.
Los dos ejes dividen el plano en cuatro partes que se llaman cuadrantes.

  Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)
J.B.Búa, Creado con GeoGebra

Prueba a cambiar la posición del punto P y fíjate cómo varían las coordenadas del punto.  Observa que, dependiendo del signo de las coordenadas, el punto se situa en una zona o cuadrante diferente.

Las funciones relacionan números con números y por tanto podemos agrupar los valores x y sus correspondientes f(x). Es decir, podemos obtener dos coordenadas para cada valor sin más que ir escribiendo (x,f(x)). En nuestro caso anterior podemos escribir fácilmente seis puntos del plano con los seis valores de los que disponemos:
 

Si representásemos los puntos (x,f(x)) en los ejes, obtendríamos lo siguiente:

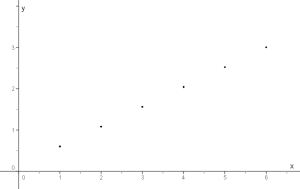
En realidad, la compañía factura de 30 segundos en 30 segundos, no cada minuto. ¿Cómo sería la función si tenemos en cuenta que el cobro por tiempo es cada 30 segundos?.

Los puntos que obtendríamos si representásemos los puntos de 30 segundos en 30 segundos sería:
 

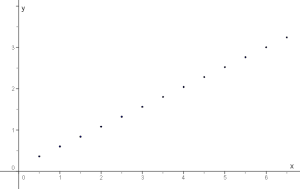
¿Y cómo sería si la compañía facturase cada segundo?:

¿Y si resultase que pudiese hacerlo a cada instante?. ¿Cuántos puntos representaríamos?:
 

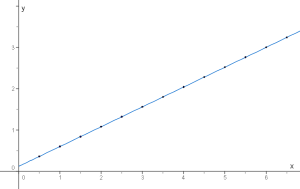
Como puedes ver, ya no son puntos aislados sino que se ha transformado en un dibujo consistente en una línea recta. Cada función da lugar a un dibujo característico al representar todos los (x,f(x)) posibles. A ese dibujo se le llama gráfica de la función y es muy importante cuando se trabaja con funciones. A los números x se le llaman orígenes y a los correspondientes f(x) imágenes. Así f(x)=x² , al origen 3 le corresponde la imagen 9 (x=3, f(3)=9).

Tanto x como f(x) son variables, es decir, números que varían. Para diferenciarlas, a x se le llama variable independiente y a f(x) variable dependiente. La razón de darles ese nombre es que el valor de x lo podemos escoger mientras que el valor de f(x) depende del valor de x que escojamos. A menudo a f(x) se le da el nombre de y. Así f(x)=x² se escribe a veces y=x²