EL
RECTÁNGULO ÁUREO Y SUS APLICACIONES EN LA SOCIEDAD
(Trabajo de Damián
Padín Santos)
Estamos rodeados de infinidad de figuras geométricas de las que no prestamos mucha atención ya que estamos más que habituados a ellas; pues bien, en este trabajo se prestará especial atención a una en particular y muy especial: el rectángulo áureo.
Si bien uno pretende una definición simple de dicha figura
geométrica esa definición sería: rectángulo cuyos lados están en proporción
áurea, es decir,
,
donde b=base del rectángulo, h= altura del rectángulo y Φ=nº irracional cuyo
valor numérico es similar a 1.618… Los griegos ya conocían perfectamente el
rectángulo áureo o rectángulo de oro, que debe su nombre a Φ (número áureo o de
oro), pues les parecía el más bello y estético y lo utilizaban en sus
construcciones. Y es que según diversos estudios se ha descubierto que las
personas cuyas caras guardan cierta simetría entre sus facciones (simetrías en
las que interviene el número áureo), son consideradas más bellas.
La cuestión que nos surge al pensar en el rectángulo áureo es: ¿de dónde sale esta figura?. Procedamos entonces a resolver esta cuestión analíticamente:
Partiendo de un cuadrado de lado x (Lado AD=AB), en donde la base se halla el punto medio E (x/2), trazamos una línea entre el punto medio y el vértice superior derecho, quedando entonces un triángulo rectángulo, que si se superpone sobre la base, da lugar a un punto fuera del cuadrado a partir del cual se construye el rectángulo áureo (punto F). Es aquí donde entra en juego la razón áurea:
|
|
 |
|
|
|
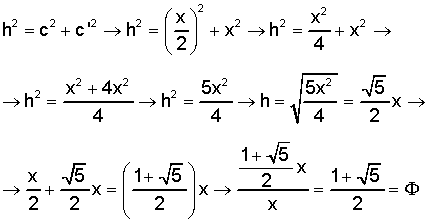Además, tiene una peculiaridad que lo diferencia de los demás rectángulos, y es que a partir de él se pueden construir innumerables rectángulos áureos quitando un cuadrado a cada rectángulo y el resultado es otro rectángulo áureo. La explicación a esta propiedad del rectángulo áureo sería: a partir de un cuadrado de lado “a”, se construye un rectángulo de lado “b” como se ha hecho en la figura 1
Entonces:
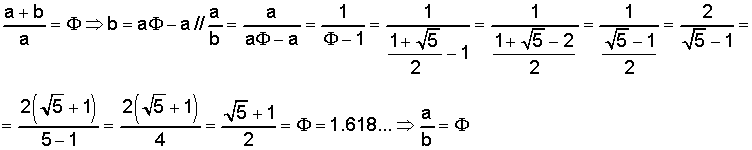
La conclusión es que el rectángulo añadido al cuadrado para formar un rectángulo áureo es nada más y nada menos que otro rectángulo áureo, a partir del cual se pueden construir infinitos rectángulos áureos.
Se han puesto diversos ejemplos de rectángulos áureos, pero, ¿de dónde sale esta figura? Procedamos entonces a resolver esta cuestión analíticamente:
Parece ser que hemos heredado aquel gusto que antes se mencionaba por el rectángulo áureo, puesto que en la actualidad utilizamos rectángulos similares para diversos productos u objetos (en principio para agradar al consumidor) tales como el D.N.I., las tarjetas de crédito o las cajetillas de tabaco.
El D.N.I. como rectángulo áureo:
A partir de la misma teoría antes mencionada, se ha creado un rectángulo áureo sobre la imagen de un D.N.I. (Fig.2) y observamos que no coinciden exactamente pero es muy similar.
Fig.2 D.N.I.
Pincha sobre la imagen para agrandar
La comprobación es la siguiente:
El D.N.I. tiene unas dimensiones (sujetas al error del calibre, cuyo margen de error es de 0.05mm) de:
Largo= 7.975cm±0.05 mm Ancho=4.85cm±0.05 mm
¿b/h=Φ?; 7.975/4.85=1.644≠Φ
Exactamente ocurre con una tarjeta de crédito, es muy similar a un rectángulo áureo pero debería ser un poco más larga, como se observa en la fig.3 ; la comprobación es la siguiente:
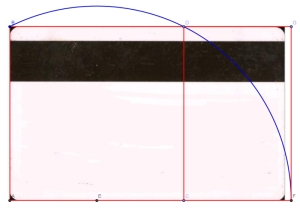
Fig.3 Tarjeta de crédito
Pincha sobre la imagen para agrandar
Largo= 8.55cm±0.05 mm Ancho=5.4cm±0.05 mm
¿b/h=Φ?; 8.55/5.4=1.644≠Φ
Se ha dejado la cajetilla de tabaco para el final ya que se trata del objeto de estudio que más se ajusta a la forma del rectángulo áureo, esto se comprueba en la fig. 4 , en la cual se observa que el rectángulo áureo construido sobre la imagen casi coincide sobre la cajetilla, y analíticamente también ocurre lo mismo:
Fig.4 Cajetilla de tabaco
Pincha sobre la imagen para agrandar
Largo= 8.865cm±0.05 mm Ancho=5.5cm±0.05 mm
¿b/h=Φ?; 8.865/5.5=1.61818≈Φ
Aquí termina este trabajo sobre el rectángulo áureo, figura creada por la naturaleza y descubierta y utilizada por la humanidad.
DAMIÁN PADÍN SANTOS
