Medida de la
circunferencia terrestre por el método de Eratóstenes
Adaptación
En la época de Eratóstenes, algunos sabios sospechaban que la Tierra tenía una forma esférica. A esta conclusión llegaban , según se dice, al observar los barcos en el océano: al acercarse el barco a tierra, se veía en primer lugar sólo el mástil y, más tarde, el casco del barco. Si la Tierra fuese plana, este hecho no se produciría y se vería el barco en su totalidad en cada momento.

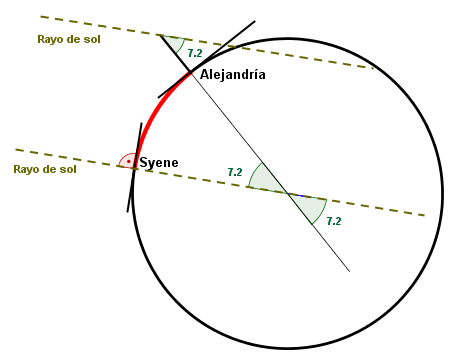
Eratóstenes, sospechando ya que la Tierra era esférica, leyó en la Biblioteca de Alejandría que en la ciudad egipcia de Syene, se observaba en el mediodía del 22 de Junio el fondo de un pozo profundo. Esa circunstancia no se daba en Alejandría.
|
|
Supuso que ese hecho significaba que el 22 de Junio los rayos de Sol llegaban con diferente inclinación a Syene y Alejandría, lo que significaba que la Tierra era curva y no plana (En Astronomía, se supone que los rayos de Sol, que llegan a la Tierra, son paralelos entre sí). Eso confirmó su sospecha de que la forma de la Tierra era una esfera.
|
|
|
Midió, el mediodía del 22 de Junio , el ángulo de inclinación de los rayos de Sol en Alejandría y obtuvo un ángulo de 7.2°. Midió también la distancia entre Syene y Alejandría, que estimó en 792.288 km. Según se dice, para calcular la distancia usó el tiempo en que las caravanas de camellos realizaban el recorrido desde Alejandría a Syene. Otras versiones sostienen que contrató a un hombre para que hiciese el recorrido contando los pasos.
Puesto que Alejandría y Syene se encuentran, aproximadamente, en el mismo meridiano terrestre, cuando el Sol pasa por el meridiano (instante que coincide con el mediodía solar), Alejandría, Syene, el Sol y el centro de la Tierra se encuentran en el mismo plano. Conociendo el ángulo de inclinación de los rayos de Sol y la distancia Alejandría-Syene, dedujo que:
![]()
Obtuvo un valor de 39 614.4 km , cometiendo un error aproximado de -0.2%, con respecto al valor real.
Adaptación:
En nuestro caso, vamos a realizar una adaptación a lo
hecho por Eratóstenes en el pasado. Realizaremos la medida del ángulo de
inclinación de los rayos de Sol coincidiendo con el mediodía solar (instante en
el que el Sol cruza la línea imaginaria Norte-Sur geográfica), pero en dos
puntos de diferentes meridianos.
Puesto que en puntos del mismo paralelo geográfico, los
ángulos de inclinación de los rayos de Sol al mediodía coinciden, podemos
calcular el ángulo de inclinación en Ferrol, por ejemplo, y será el mismo que el
ángulo de inclinación del punto que se encuentra en el mismo paralelo que Ferrol y el mismo meridiano que
Cambados. De esa forma Ferrol "trasladado",
Cambados el Sol y el centro de la Tierra, estarán en el mismo plano.
Deberemos, por tanto, medir la distancia X, entre un punto (B), y A "trasladado" al meridiano de B (A’).
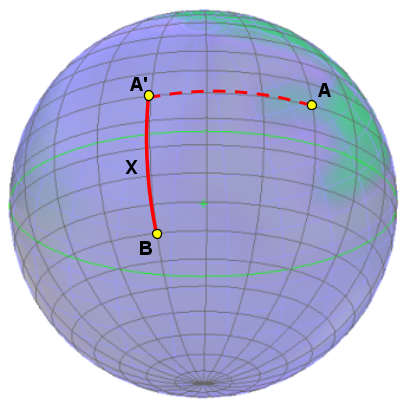
Una vez medida esa distancia, deberemos medir los ángulos en los dos centros al mediodía solar, α y β
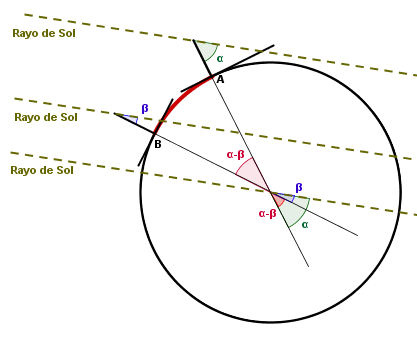
![]()
Siendo:
A el "trasladado" de uno de los centros (Ferrol, por ejemplo) sobre el meridiano del centro B
B el centro de referencia (Cambados, por ejemplo)
a el ángulo de inclinación de los rayos de Sol respecto a la vertical en el centro A
b el ángulo de inclinación de los rayos de Sol respecto a la vertical en el centro B
Alumnos participantes. Picar para ampliar