Cuad. Mat. Pir. Kheops

Una vez nivelado el terreno, los egipcios debieron marcar sobre el suelo la base de su pirámide. La base es un cuadrado de unos 230 m de largo y como medir distancias no representa una dificultad, el problema fundamental es determinar un ángulo de 90°. Entre todas las posibilidades para el trazado de un ángulo de 90°, los arqueólogos barajan tres posibilidades como las más probables (ver artículo de la web egyptour):

- La primera es el uso de la terna 3,4,5. Por tratarse de una terna que cumple el teorema de Pitágoras, un triángulo con esos lados posee unos de sus ángulos igual a 90°. Se supone que los egipcios conocían el hecho de que un triángulo de lados 3,4 y 5 determinaba un ángulo de 90° y que usaban este hecho mediante una cuerda de 12 nudos. Al unir los extremos de la cuerda y disponerla de forma que formase un triángulo donde los lados contuviesen 3, 4 y 5 nudos, el triángulo resulta rectángulo. No es, desde luego, la única terna que cumple esta propiedad. Aquellas ternas que cumplen el teorema de Pitágoras se las conoce como ternas pitagóricas y el hecho de que determinen un triángulo rectángulo se conoce como "Teorema inverso de Pitágoras".

- La segunda posibilidad barajada es el uso de una escuadra dispuesta sobre un palo colocado verticalmente al suelo.

- La tercera posibilidad se basa en el trazado clásico de la mediatriz de un segmento. Dicha mediatriz forma 90° con el segmento lo que representa que si trazamos una mediatriz, determinamos en el proceso un ángulo de 90°.

A los alumnos, sin informarlos de todos estos hechos, se les propuso que pensasen un sistema que permitiese trazar sobre el terreno un ángulo de 90° que, a su vez, sirviese para trazar un cuadrado de grandes dimensiones. El primer alumno en proporcionar un método fue, nuevamente, Pablo Chaves Pintos. Su método representaba una variante del método descrito con la terna 3, 4 y 5 pero usando la terna, en su idea original, 60, 80, 100. La alumna Alba González Rivas se presentó voluntaria para buscar la forma de usar el método del trazado de una mediatriz. A continuación se pueden leer sus trabajos y los resultados obtenidos usando ambos métodos.

Para realizar un ángulo de noventa grados sobre un terreno o bien un cuadrado solo debemos tener en cuenta algo imprescindible, es decir, poder llevar a cabo un sistema fiable que a partir de una línea trazada nos permita realizar un ángulo recto y que nos sirva para grandes y pequeñas superficies. Uno de los métodos más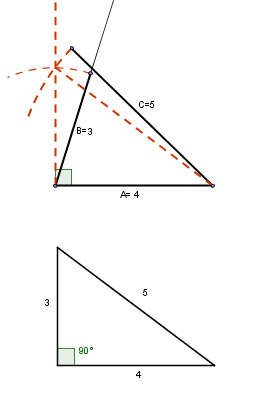 fiables que podemos realizar es una Terna Pitagórica que al basarse en el teorema de Pitágoras, tres enteros positivos a, b, c que cumplen que a² + b² = c², nos debería de dar un ángulo recto perfecto.

Para llevar a cabo el proceso trazamos una línea recta de cuatro metros con un cordel amarrado a dos piquetas(A), una vez hecho esto y asegurarnos de que el cordel está bien tenso, nos situamos en una de las piquetas para volver a atar otro cordel en esa misma piqueta(B) y cortamos el cordel un poco más largo que el primero.

Ahora tenemos un cordel de 4 metros(A) que traza una línea recta horizontal y otro en una de sus esquinas que está suelto(B), pues bien, ahora nos vamos al otro lado del cordel que esta tenso(A) y volvemos a atar otro cordel(C) pero de esta vez no cortamos, lo dejamos largo. Una vez hecho esto tenemos el cordel (A) que traza una línea recta de cuatro metros y otro en una de sus esquinas(B), pues ahora vamos al cordel (B) y medimos tres metros y hacemos una marca.

Es ahora cuando en el cordel (C) realizamos la marca de los cinco metros. Cuando ya tenemos todo esto hecho, juntamos el cordel (B) y el cordel (C) haciendo coincidir las marcas de cada uno y formaremos un triangulo con lados (3 metros,4 metros y 5 metros), que si está bien hecho nos formara un ángulo de noventa grados ya que:

Ya sabemos que teóricamente este resultado sería prácticamente perfecto, pero al llevarlo a la práctica en cada paso, que suelen ser poco precisos, estos pequeños errores nos conllevan a un resultado final un poco desviado de los resultados esperados. Tanto es así que el resultado obtenido del ángulo hecho ha sido de (89.549˚). Para saberlo utilizamos un laser que nos marcó justo donde tenía que ser el ángulo recto.
Para poder conocer nuestro error utilizamos un nivel laser que nos halló la marca exacta de los 90˚, conociendo la posición del ángulo recto dado por el láser y la marca de los supuestos 90˚ hecha por nosotros, solo queda restarlas.

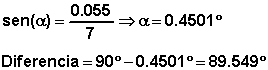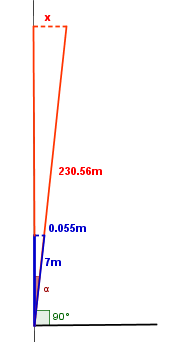A partir de estos resultados y haciendo referencia a la base de la pirámide, hemos calculado el error que cometeríamos si en vez de llevarlo a cabo con esas medidas, lo hubiéramos hecho con la medida de la base de la pirámide. Obviamente el error sería mucho más grande en comparación con nuestras medidas. Mediante una regla de tres podemos calcularlo y es lo siguiente:

Si en siete metros erramos 0.055 metros, en 230.56 metros (medida del lado de la pirámide de Kheops) erraremos x metros.

= 1 metro y 81 cm de error que cometeríamos en las dimensiones del lado de la pirámide.


Pincha en las imágenes para agrandar

MEDIDA DE UN ANGULO DE 90 ˚ SOBRE UN TERRENO
por Alba González Rivas

Para hacer un ángulo recto sobre el terreno:

1º Clavamos dos palos a una cierta distancia, que no tiene porque ser conocida, y los unimos con una cuerda.

2º Cogemos dos cuerdas de la misma longitud, y que sean más largas que la mitad de la primera cuerda. Atamos una cuerda a cada palo.

3º Movemos las dos cuerdas, hacia a un lado, intentando que vayan al mismo nivel, y en el punto donde se cruzan clavamos un palo.

4º Hacemos lo mismo hacia el otro lado.

5º Unimos con una cuerda los dos palos y ya tenemos el ángulo de 90º.

Medida del error cometido. Datos recogidos con ayuda de un nivel láser, usado para fijar el ángulo de 90^o

cateto opuesto/hipotenusa = seno A

0.19/4.72= 0.04025

seno A = 0.04025

A = 2.3070^o

El error cometido al medir el ángulo fue de 2.3070^o


Pincha en las imágenes para agrandar